software + analysis:
Eclipse Timing Variations
Studying the gravitational effects of three body dynamics.
Studying dynamical effects
The orbiting motion of multiple stars produces observable dynamic effects in the time-series brightness measurements of stars. I built a generalized probabilistic model that predicts the observable effects of this motion in multiple types of astronomical time-series data, using symbolic coding tools including pyMC. The code uses numeric sampling tools, such as Hamiltonian Monte Carlo, to derive parameter inferences of the physical stellar system by modeling the data.
Software overview: signal extraction
The open-source software code has two parts. The first part evaluates the TESS light curve in order to precisely determine the timings of each of the eclipses.
In brief, the code generates a model of the primary eclipse by fitting a trapezoid or cosh function (the shapes found to best represent eclipses) to the smoothed, phase folded and subsequently binned time-series data. This model is then fit to each individual primary eclipse where the only two free model parameters are the time of eclipse and the slope of an underlying linear trend. The latter is to allow for systematic effects that change the slope of the eclipse. The same methodology is independently carried out for the secondary eclipses. The individual fits to all eclipses, including both the primary and the secondary eclipses are optimized using a Markov chain Monte Carlo (MCMC) approach, using the open source software EXOPLANET (Foreman-Mackey et al. 2021). The observed minus calculated times of eclipse (O – C) can be used to study the dynamical effects caused by a third body in the system.
Software overview: data modelling
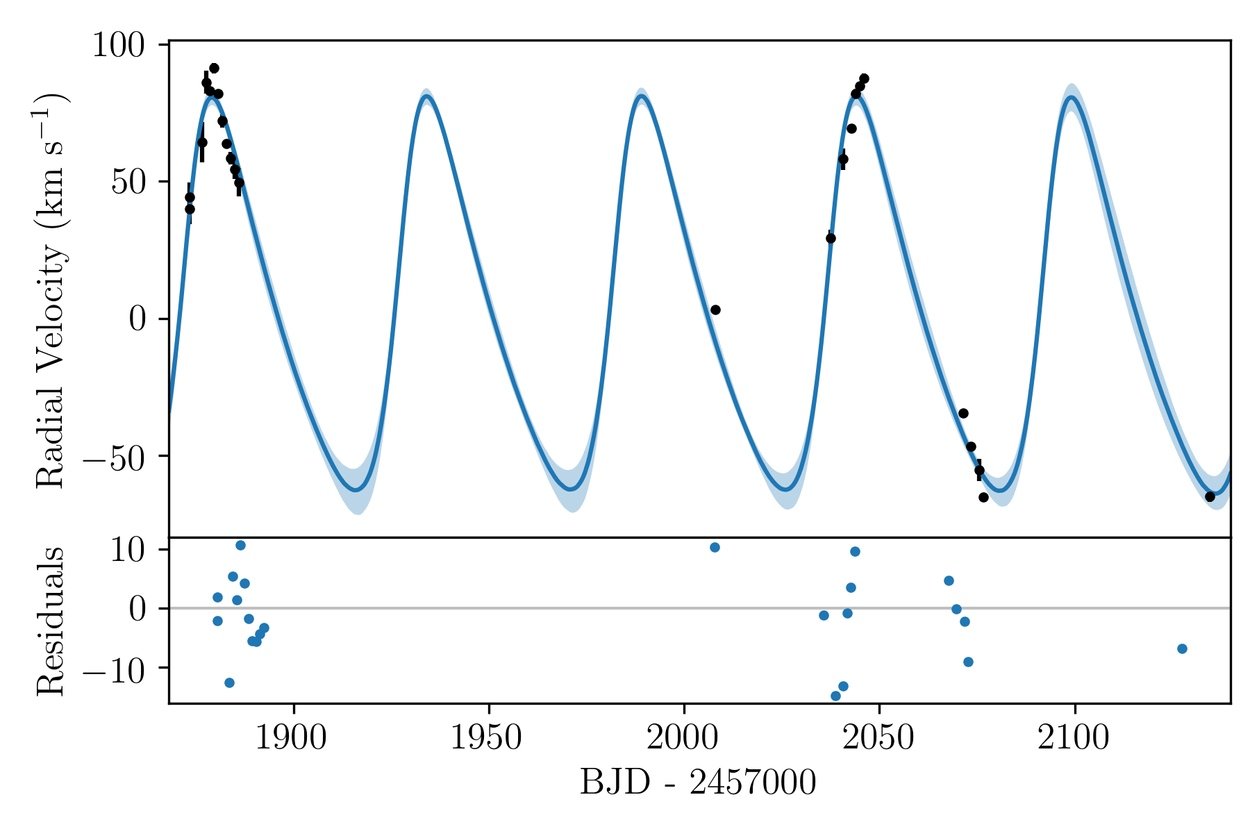
There are two main effects responsible for deviations from strict periodicity in eclipse timings: the light travel time effect (LTTE; geometrical contribution) and the dynamical effect. The former is a result of a change in projected distance from the centre of mass of the binary to that of the triple. The dynamical effect, on the other hand, results from physical changes in the orbit of the binary system due to the gravitational influence of the third body (Borkovits et al., 2003). Modeling of the LTTE and dynamical eclipse timing variation effect allows us to derive properties including the mass ratio of the tertiary (outer most star) to the total mass of the system, the eccentricity of the tertiary, and the mutual inclination between the orbital plane of the binary and the orbital plane of the tertiary.
The second part of the software jointly models the eclipse timing variations and radial velocity data, following the methodology outlined in Borkovits et al. (2016).
The model optimisation is carried out using a No U-Turn Sampling (NUTS; Hoffman & Gelman, 2011) Hamiltonian Monte Carlo (HMC) approach. In short, HMC is a class of MCMC methods used to numerically approximate a posterior probability distribution. However, whereas traditional MCMC techniques use a stochastic walk to explore a given n-dimensional parameter space, the HMC algorithm makes use of a Hamiltonian description of probability distribution in order to more directly sample the posterior probability distribution of a set of model parameters, given by Bayes’ theorem. While the standard HMC approach requires a manual fine-tuning of the number of steps and step sizes in which the system is evolved, making it very inefficient, the NUTS HMC sampler evolves the system until the proposed location starts to revert towards the initial location. Furthermore, the NUTS sampler adopts the random adopt/reject approach of new locations that is used by the standard MCMC algorithm. The NUTS sampler is used for the analysis as it is more time efficient than the standard MCMC approach for exploring high dimensional parameter spaces.